Analytical view to trigonometry
I apply trigonometry differently than school teached it to me. There's night/day difference between how it was taught in school and how I'm using it in programming. I'm curious whether I could teach that viewpoint ahead.

If you take a two-dimensional cartesian coordinate grid and a vector using those coordinates as a basis. Lets assume you know all values in this problem and have labelled them:
c, The length of the vector.a.l,a.r, Both left and right -hand side angles between the x -axis and the vector.x, The x-coordinate of the vector.y, The y-coordinate of the vector.
The trigonometry states completely how these values relate:
- x = c * cos(a)
- y = c * sin(a)
- y = tan(a) * x
Note that these equations do not denote whether they are left or right-handed. The angle depends on where Y-axis on your basis points to. If the y-coordinate is on the left side of X, the angle in trigonometry function is the left-hand angle.
Since sum of left-hand and right-hand angles forms a full circle. You know both angles if you know either one. Therefore it is neat to denote that 'a' means either one depending on which side your Y-axis points to.
If you want to draw this, you only need to know two of the values we know here. That means you can always determine the remaining two values if you already know two of them.
Together with Pythagorean theorem, and what is described on this page, you have powerful and compact kit for solving vast array of geometric problems.
Exercises
Unfortunately you can't truly understand something you never strain your brain with, no matter how simple it was. For that you need good exercises.
You could invent your own exercises, but doing so you might invent something you can't solve with just trigonometry and pythagorean theorem. Therefore I advice you won't try to search for solution on these exercises so you won't lose an opportunity to learn what you supposed to.
Remember to check your results few times before you accept your conclusions. Do some calculations with calculator and check that they're consistent. Then repeat your line of thought.
Exercise 0: bent strip of paper
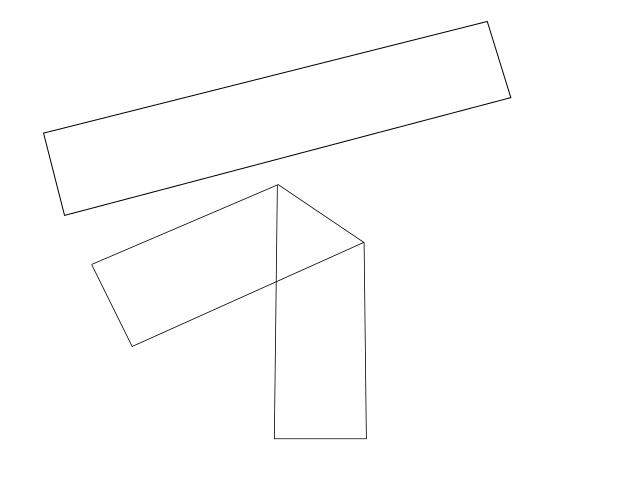
- Take a strip of paper that has uniform width like below.
- Bend it once.
- Label dimensions that you can roughly measure, then determine analytically how they relate.
Exercise 1: triangulation
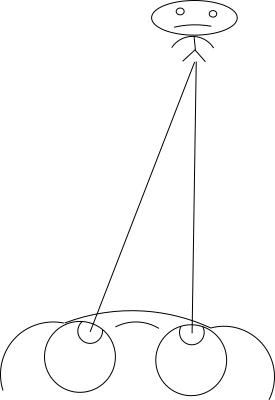
My sanity started to give out at this point, so in the illustration you have giant frog shooting artillery fire from her eyes. To hit she needs to know how far her victim is so she triangulates them.
If you draw different frogs and victims, make sure the line of sight to victim is straight with a ruler, and that it's easy to measure where the frog is facing. Again you can see all the values, unlike the frog, determine how they relate and you made this exercise.
Exercise 2: rolling triangles
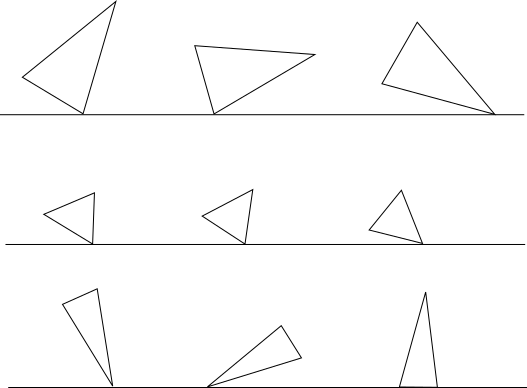
Unfortunately my imagination started to give at this point. But here's yet one. You have triangles that roll along a path like that. You may cut several triangles from paper to come up with your own.
This is even harder than the two before it. Now you've got motion along the problem, and you possibly also have to find out what to measure in the pictures you have.
Otherwise it's same. Considering this scenario, imagine what kind of relations it'd follow.
Exercise 3: circle on circular orbit
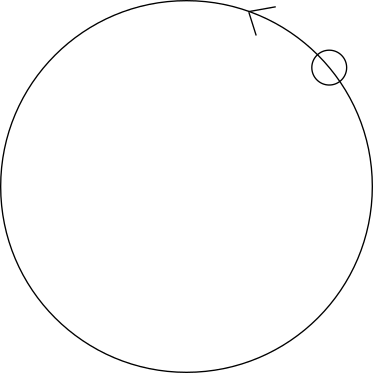
Imagine you've got a circle like this travelling on a circular orbit. The arrow points out how fast it is orbiting and to which direction. It might also be a pen strung to a string.
ATTENTION Achtung: You may end up drawing sunflowers or daisies if you are not careful. Either that happens, or then you know differentiation with polar coordinates. In that case I advice you don't try this last exercise.
Important
Angles on computers aren't described in degrees. Rather they are described as unit arc lengths.
If you had an infinite toilet roll that would never run out of paper and always stood in your unit length radius. Aside from being an amazing magical artifact that caused thousand wars eventually destroying every civilization that sought for good writing material. It would also work to describe how the angles are described on computers:
